The code for this project can be found on it’s github repo

Introduction

I read this paper a while ago and thought the problem it looked at was really interesting. It seems like it might be nice to see if RL could be applied to generating synchronization. This is an interim post looking at the implementation of the model, which will hopefully be used as a RL training environment.

Theory

As per the linked paper, this model models firefly swarms which synchronize their light flashes in a distributed manner. In the model nodes represent fireflies, and each firefly fires/flashes based on its phase $\phi(t)$ and threshold phase $\phi_{t}$. In isolation a fireflies phase increases linearly over time until it reaches $\phi_{t}$ where the firefly fires and resets its phase to 0 (i.e. in isolation the firefly will oscillate firing at regular intervals).

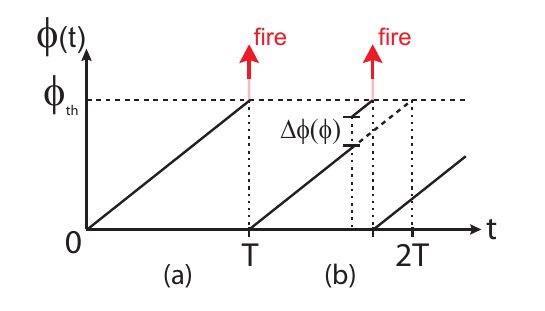
Time evolution of the phase. With no observed events (a) $\phi$ increases linearly until $\phi_{t}$ at which point if fires and resets. When a signal is observed (b) $\phi$ is incremented by $\Delta\phi(\phi).$ Image taken from 'Firefly Synchronization in Ad-Hoc Networks': Tyrell, Bettstetter & Auer, 2006.
Time evolution of the phase. With no observed events (a) $\phi$ increases linearly until $\phi_{t}$ at which point if fires and resets. When a signal is observed (b) $\phi$ is incremented by $\Delta\phi(\phi).$ Image taken from 'Firefly Synchronization in Ad-Hoc Networks': Tyrell, Bettstetter & Auer, 2006.

In an effort to co-ordinate their flashes the fireflies react to flashes from other fireflies, updating their phase as $\phi\rightarrow\phi+\Delta\phi$ where the update depends on the current phase

\[\phi+\phi\Delta\phi = \text{min}(\alpha\phi+\beta, 1)\]

where

\[\alpha=\exp(b\epsilon) \quad\text{and}\quad\beta=\frac{\exp(b\epsilon)-1}{\exp(b)-1}\]

In the case the signals are instantaneous the synchronization eventually always occurs. The more interesting case is where there are delays in the signal (or this could be thought of as a finite propagation speed).

Implementation

Given the longer term goal of using this as an RL training environment time is discrete, with all nodes updated at each step. In the case that signals propagate instantly this model would be almost trivial to implement. Simulating delayed signals is done by placing events in the future of each node, so they are processed with a delay as the model steps forward.

The model is initialized for a fixed number of steps $s$ and $n$ nodes along with:

  • A $s\times n$ array $P$ storing the phase of each node at time step $t$ of the model
  • A $n\times n$ distance matrix $D$ representing the transmission time between each pair of nodes
  • A $(s+\max(D))\times n$ array that will track events observed by each node. The additional $max(D)$ rows are required to always allow events to set in the future of each node.

The threshold phase $\phi_{t}$ is fixed at $1$, so the size of a time step is effectively controlled by a parameter $\delta\phi$ which is the amount the phase is increase for each node when no signal is observed

\[\phi(t) = \phi(t-1)+\delta\phi\]

At each step the model then advances using (in pseudocode)

for each node
    if phase >= threshold -> phase = 0

for each node
    if phase == 0
        for each node x (not including this node)
            increment the number of events for x at time t+distance

step <- step+1

for each node
    if events[t][node] > 0 
        node-phase = phase_update(phase)
    else
        node-phase = node-phase + delta-phase

effectively at each step, the nodes fires if its phase is at the threshold value. This firing places an event at step $t+\text{distance}$ for each node (the events are then effectively in the future of each node as we step the model forward). We then advance time and check if any events have been observed and update each nodes phase accordingly.

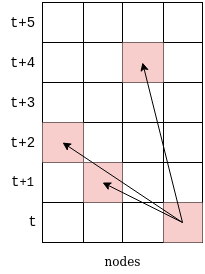
Events produced by a node are placed in the future of other nodes in the model to simulate delays in signals
Events produced by a node are placed in the future of other nodes in the model to simulate delays in signals

Note: This does have the drawback that event distances have to be integer values (as it then informs where in the array to add the event). Events have to be placed at minimum size of $1$ to be seen. This does mean a distance $0$ can be used to implement a lack of communication between nodes.

This implementation has been chosen with a couple of things in mind:

  • Using this as an RL environment will be easier updates are step based.
  • Implemented in numpy with pre-allocated arrays for the state of the model is pretty fast. I think this could be done for continuous time with appropriate scheduling of the event observation, but feel it would be a lot more computation to handle queues of events for each node.

Conclusion

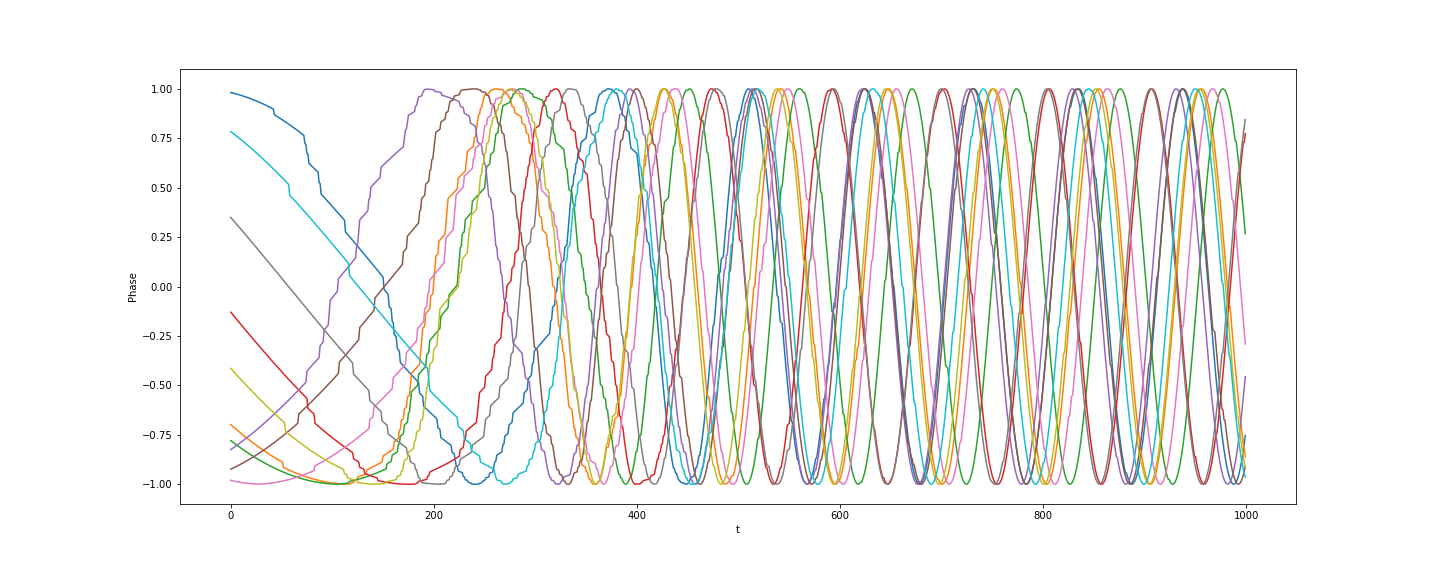
Phase evolution over time represented by $\cos(\phi(t)))$ for a subset of nodes showing how nodes react to signals.
Phase evolution over time represented by $\cos(\phi(t)))$ for a subset of nodes showing how nodes react to signals.

The real trick in this model was modelling the delay/travel time of signals by placing events in the future of each node. It’s interesting to see how the co-ordination breaks down as signal delays increase, or gaps are created in the network.

As noted in the introduction I’d like to use this to train an RL model at a node level, that is the agent should choose how to update it’s phase given the current phase and observed events, and if this results in global coordination.

The code to run the current model,and examples of usage can be found on the github repo.